TEOREMA DE NAPOLEÓN

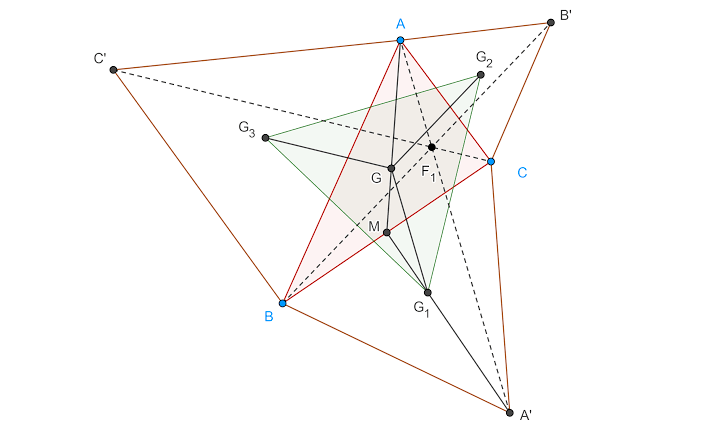
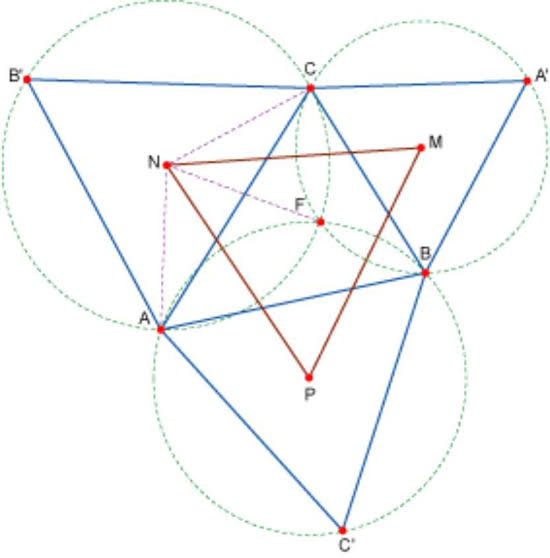
El teorema de Napoleón establece que si se construyen triángulos equiláteros, ya sean todos internos o externos los centros de estos triángulos equiláteros formarán un nuevo triángulo equilátero.

HISTORIA DEL TEOREMA DE NAPOLEÓN

Historia incierta.
Aun que principalmente el Teorema se ha atribuido al propio Napoleón Bonaparte por la conciencia en el nombre, es cierto que no existen datos históricos que verifiquen que el emperador Frances es el auténtico autor de ese resultado matemático. De hecho, parece ser que la primera vez que apareció una mención del Teorema fue una publicación en el año 1825, cuatro años despues de la muerte de Bonaparte, en la revista The Ladies' Diary, como una pregunta planteada por el matemático ingles William Rutherford (aunque no te suene su nombre, este hombre fue el primero en calcular los primeros 208 dígitos del número pi en el año 1841).

En realidad, se piensa que las capacidades de William Rutherford eran muy altas, por lo que, probablemente, esa pregunta fuera solo una cuestión a la cual el ya tenia la respuesta. Por esta razón se piensa que podria haber sido el propio William el autor del Teorema, pero el hecho de haber sido coetáneo a Napoleón Bonaparte y de que no haya ninguna verificación al respecto, no permite la confirmación de ninguna teoria.

FORMULA DEL TEOREMA DE NAPOLEÓN.

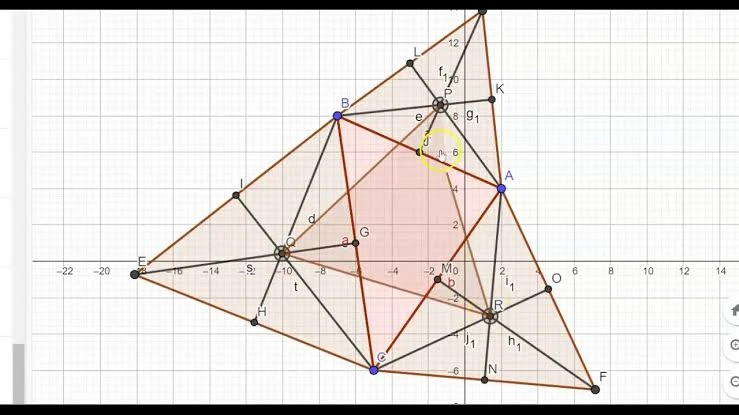
El teorema de Napoleón establece que si se construyen triángulos equiláteros sobre los lados de un triángulo cualquiera y se conectan los centros de estos triángulos equiláteros, se forma otro triángulo equilátero. Este nuevo triángulo se conoce como el triángulo de Napoleón. No hay una formula en sí, si no una construcción geometrica que resulta en un triángulo equilátero.
Los pasos para llegar a este, son:

1.Triangulo de partida.

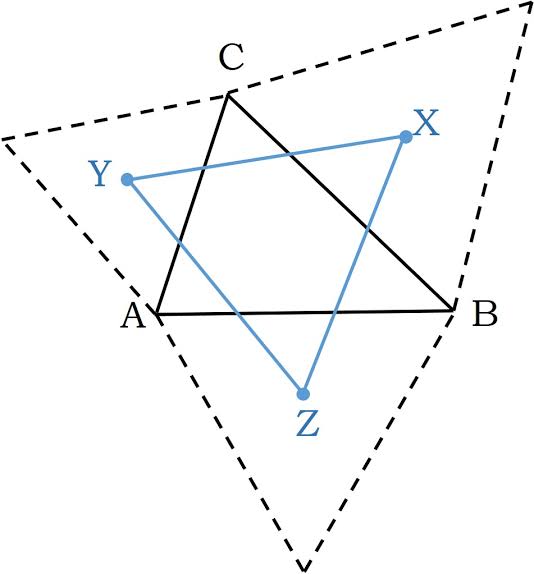
Empieza con un triángulo arbitrario (el que sea) con el que empezaremos con ABC.

2.Triangulos equiláteros.

Sonbre cada lado del triángulo ABC (externamente), construye un triángulo equilátero, este significa que en AB se construye con triangulo ABZ, sobre BC se construye un triángulo BCX y sobre CA se construye un triángulo CAY.

3.Centro de los triángulos.

Calcula los centros de cada uno de los triángulos equiláteros (ABZ, BCX, CAY). Estos puntos son los puntos donde se intersectan las medidas de cada triángulo equilátero.

4.Triángulo de Napoleón.

Conecta los centros de los triángulos equiláteros (Z, X, Y), el triangulo formado (ZXY) es también un triángulo equilátero apesar de cualquier movimiento existente.

EL TEOREMA DE NAPOLEÓN NO INVOLUCRA UNA FÓRMULA MATEMÁTICA ESPECÍFICA, si no que describe una construcción geométrica donde la unión de los centros de los triángulos equiláteros construido sobre los lados de un triangulo arbitrario siempre resulta de un nuevo triángulo equilátero.

FORMAS DE USO DEL TEOREMA DE NAPOLEÓN

Función practica:

El teorema de Napoleón, aun que principalmente geométrico, tiene algunas conexiones interesantes con la vida cotidiana, especialmente en áreas relacionadas con la construcción y el diseño. Aun que no se utiliza directamente como una herramienta práctica en tareas diarias, su principio de formas un triángulo equilátero a partir de otros triángulos equiláteros construidos sobre los lados de un triángulo inicial puede inspirar enfoques en la resolución de problemas de diseño y optimización.

Aplicaciones indirects:

Diseño arquitectonico y de ingeniería:
El teorema al explorar la relaciones entre formas geométricas puede servir como inspiración para la creación de estructuras estables y equilibradas, donde la simetría y las relaciones entre sus componentes son clave.
Diseño grafico y artístico:
La idea de formar figuras regulares a partir de otras puede ser útil en el diseño de logotipos, patrones y otras composiciones visuales que buscan armonía y equilibrio estetico.
Resolución de problemas de optimización:
En situaciones donde se busca la máxima eficacia a la mejor distribución espacial, la lógica subyacente al teorema puede ayudar a encontrar soluciones óptimas en el diseño de espacios o sistemas.

Aun no es una herramienta práctica de uso común, el teorema de Napoleón puede influir en la forma en la que se abordan problemas de diseño y optimización, especialmente en áreas donde la geometría y las relaciones espaciales son importantes.